1135 Is It A Red-Black Tree (30分)

There is a kind of balanced binary search tree named red-black tree in the data structure. It has the following 5 properties:

(1) Every node is either red or black.
(2) The root is black.
(3) Every leaf (NULL) is black.
(4) If a node is red, then both its children are black.
(5) For each node, all simple paths from the node to descendant leaves contain the same number of black nodes.
For example, the tree in Figure 1 is a red-black tree, while the ones in Figure 2 and 3 are not.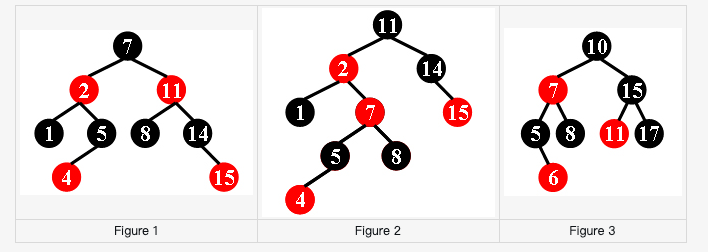

For each given binary search tree, you are supposed to tell if it is a legal red-black tree.

Input Specification:

Each input file contains several test cases. The first line gives a positive integer K (≤30) which is the total number of cases. For each case, the first line gives a positive integer N (≤30), the total number of nodes in the binary tree. The second line gives the preorder traversal sequence of the tree. While all the keys in a tree are positive integers, we use negative signs to represent red nodes. All the numbers in a line are separated by a space. The sample input cases correspond to the trees shown in Figure 1, 2 and 3.

Output Specification:

For each test case, print in a line “Yes” if the given tree is a red-black tree, or “No” if not.

Sample

Input:

3
9
7 -2 1 5 -4 -11 8 14 -15
9
11 -2 1 -7 5 -4 8 14 -15
8
10 -7 5 -6 8 15 -11 17

Output:

Yes
No
No

Solution

关于红黑树的定义参照 (rb_tree)

了解了红黑树的定义后，步骤就很清晰了

1. 建树（采用链表或者数组均可以）
2. 判断是否为红黑树，主要抓住一下几点
   1. 根节点为黑色
   2. 每个节点非黑即红
   3. 红色节点是叶子结点或者它的孩子节点（左右） 均为黑色节点
   4. 每个节点的左右节点的黑高均相等

Code

struct RBNode
{
    struct RBNode *left, *right;
    int key;
};

int getheight(RBNode *root)
{
    if (!root)
        return 0;
    int l = getheight(root->left);
    int r = getheight(root->right);
    return root->key > 0 ? max(l, r) + 1 : max(l, r);
}

RBNode *insertRBTree(RBNode *root, int val)
{
    if (!root)
    {
        root = new RBNode();
        root->left = root->right = nullptr;
        root->key = val;
    }
    else
    {
        if (abs(val) <= abs(root->key))
        {
            root->left = insertRBTree(root->left, val);
        }
        else
            root->right = insertRBTree(root->right, val);
    }
    return root;
}

// 判断是非为 rb tree
bool isRBTree(RBNode *root)
{
    // 采用 层序遍历 来判断是否符合要求
    queue<RBNode *> q;
    q.push(root);
    bool is = true;
    while (!q.empty() && is)
    {
        RBNode *node = q.front();
        q.pop();
        if (node->left)
        {
            q.push(node->left);
        }
        if (node->right)
        {
            q.push(node->right);
        }
        int left = getheight(node->left), right = getheight(node->right);
        if (left != right)
            is = false;
        if (node->key < 0)
        {
            if (!((!node->left && !node->right) || (node->left && node->left->key > 0 && node->right && node->right->key > 0)))
                is = false;
        }
        else if (node->key == 0)
            is = false;
    }
    return is;
}

void pat_1135()
{
    int k, i, j, n, val;
    cin >> k;
    for (i = 0; i < k; i++)
    {
        cin >> n;
        RBNode *root = nullptr;
        for (j = 0; j < n; j++)
        {
            cin >> val;
            root = insertRBTree(root, val);
        }
        if (root->key < 0 || !isRBTree(root))
            cout << "No" << endl;
        else
            cout << "Yes" << endl;
    }
}

int main()
{
    pat_1135();
    return 0;
}