position encoding in attention

为什么需要 position encoding ？

Attention 无法捕捉输入顺序，即无法区分不同位置的Token，缺乏对不同Token之间位置信息的建模

self-attention

attention

q,k,v 代表 query、key、value 矩阵或者向量

相似度矩阵 affinity matrix

最后的输出:
$$
\begin{equation}
v^{‘}{i} = \sum{i=1}^n
\end{equation}
$$

position encoding 分类

绝对位置编码 absolute position encoding

直接在输入序列上加上相同维度的 matrix 或者 vector p， p 分为两种：可学习的和不可学习的

代表输入的序列， T 为序列长度， D 为每一输入向量（Token）的维度。代表位置编码，它的维度与x相同。

matrix expand for absolute position encoding

对绝对位置编码进行矩阵展开:

带入到:

来计算 affinity matrix A 的某一项:
$$
\begin{equation}
\begin{aligned}
A_{ij} &= q_i^Tk_j \
&= (W_q(x_i + p_i))^T(W_k(x_j + p_j)) \
&= (W_qx_i + W_qp_i)^T(W_kx_j + W_kp_j) \
&= (x_i^TW_q^T + p_i^TW_q^T)(W_kx_j + W_kp_j) \
&= x_i^TW_q^TW_kx_j + \underbrace{x_i^TW_q^TW_kp_j}{(1)} + \underbrace{p_i^TW_q^TW_kx_j}{(2)} + \underbrace{p_i^TW_q^TW_kp_j}{(3)} \
&= A{o} + PE_{j} + PE_{i} + PE_{ij}
\end{aligned}
\end{equation}
$$

在(1)、（2）、（3）处进行排列组合可以得到相对位置编码和混合位置编码.

相对位置并没有完整建模每个输入的位置信息，而是在算Attention的时候考虑当前位置与被Attention的位置的相对距离(i, j)，由于自然语言一般更依赖于相对位置，所以相对位置编码通常也有着优秀的表现。对于相对位置编码来说，它的灵活性更大，更加体现出了研究人员的“天马行空”。 From 苏剑林

Learnable Absolute Position Encoding

出自《Convolutional Sequence to Sequence Learning》中的可学习的位置编码

直接将位置编码 p 当成参数来参与训练.

Fixed Absolute Position Encoding

Vanilla Transformer位置编码

2i 是指偶数位， 2i+1 奇数位， t 是指位置， d是指向量的维度

相对位置编码 relative position encoding

learnable : Swin Transformer

相同的相对位置采用同一个编码

去掉了（1）、（2）处的位置编码，将（3）变成一个learnable PE ，并加在了 Affinity Matrix 上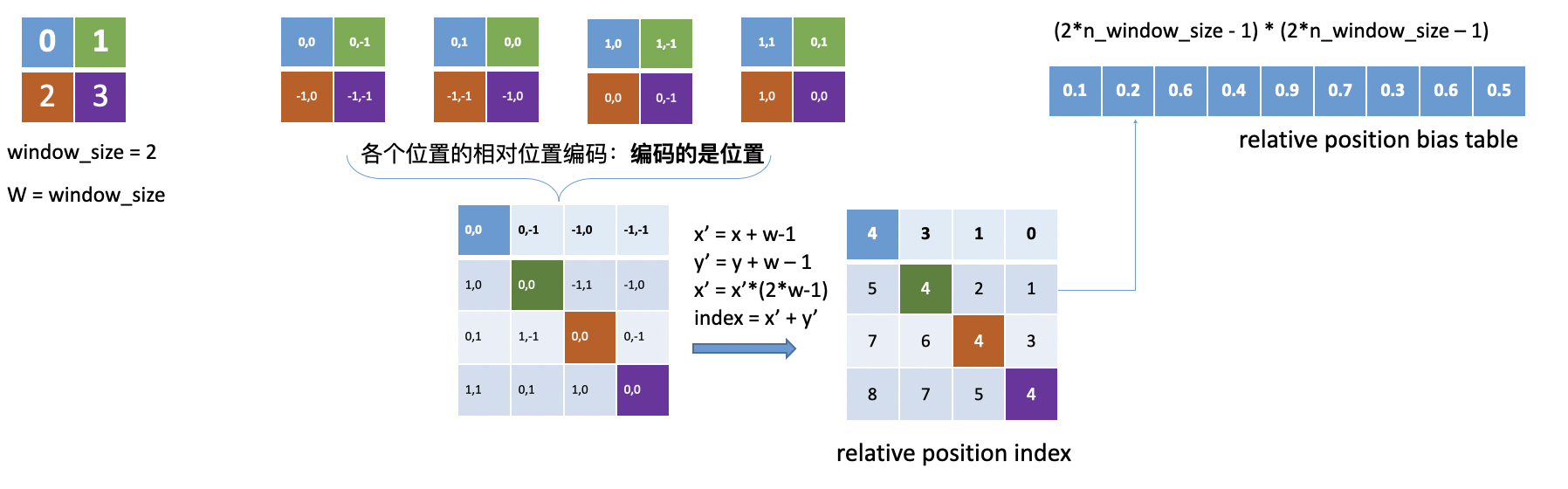

相对位置只有 [-(window_size - 1), window_size - 1]个，各个相对位置之间的位置编码
为(2window_size - 1)(2*window_size - 1)